Probabilidade em Genética

 

Introdução

O quadro de Punnett é uma ferramenta valiosa, mas não é ideal para todos os problemas genéticos. Por exemplo, suponha que te peçam para calcular a frequência da classe recessiva, não para um cruzamento Aa x Aa, não para um cruzamento AaBb x AaBb, mas para um cruzamento AaBbCcDdEe x AaBbCcDdEe. Se você quisesse resolver essa questão usando o quadro de Punnett, você poderia – mas você precisaria completá-lo com $1024$1024 caixas. Provavelmente, algo que você não queira fazer durante uma prova ou qualquer outro momento, se puder evitar!

O problema acima, envolvendo cinco genes, se torna menos intimidante quando você percebe que o quadro de Punnett é apenas uma forma visual de representar cálculos probabilísticos. Apesar de ser uma ótima ferramenta quando você está trabalhando com um ou dois genes, pode se tornar lenta e trabalhosa à medida que o número aumenta. Em algum momento, se torna mais rápido (e com menos tendência ao erro) simplesmente fazer o cálculo probabilístico, sem a representação visual do quadro de Punnett. Em todos os casos, os cálculos e o quadrado fornecem a mesma informação, mas ao ter ambas as ferramentas, você estará preparado para lidar com um número maior de problemas de uma forma mais eficiente.

Neste artigo, vamos rever alguns fundamentos da probabilidade, inclusive como calcular a probabilidade de dois eventos independentes ocorrerem (evento X e evento Y) ou a probabilidade de ocorrer um de dois eventos mutuamente excludentes (evento X ou evento Y). Depois, vamos ver como esses cálculos podem ser aplicados a problemas genéticos, e mais especificamente, como podem ajudá-lo a resolver seus problemas envolvendo números relativamente grandes de genes.

[Solução do problema do cruzamento dos cinco genes]

Fundamentos da probabilidade

Probabilidades são medidas matemáticas de possibilidades. Em outras palavras, são uma forma de quantificar (dar um valor numérico específico) o quão provável é um acontecimento. A probabilidade de $1$1 para um evento significa que é garantido que ele vai ocorrer, enquanto a probabilidade de $0$0, significa que seguramente não vai ocorrer. Um exemplo simples é ter 50% ou $1/2$1, slash, 2 das chances de tirar coroa quando você joga uma moeda, como Sal explica neste vídeo introdução a probabilidade.

As probabilidades podem ser empíricas, ou seja, calculadas a partir de observações do mundo real, ou teóricas, ou seja, estimadas usando um conjunto de regras ou pressupostos.

• A probabilidade empírica de um evento é calculada contando-se o número de vezes que o evento ocorreu e dividindo esse valor pelo número total de vezes que o evento poderia ter ocorrido. Por exemplo, se o evento que você está buscando fosse o de uma ervilha com semente rugosa e você a viu $1{.}850$1, point, 850 vezes de um total de $7{.}324$7, point, 324 sementes examinadas, a probabilidade empírica de se ter uma ervilha de semente rugosa seria de $1{.}850/7{.}324 = 0{,}253$1, point, 850, slash, 7, point, 324, equals, 0, comma, 253, ou muito perto de $1$1 em $4$4 sementes.
• A probabilidade teórica de um evento, por sua vez, é calculada com base em informações sobre as regras e circunstâncias que produzem o evento. Esse tipo de probabilidade reflete o número de vezes que espera-se que um evento ocorra em relação ao número de vezes que ele poderia ocorrer. Por exemplo, se você tivesse uma planta de ervilha heterozigota para o gene da forma da semente (Rr) e a deixasse realizar autofecundação, você poderia usar as regras da probabilidade e seu conhecimento de genética para prever que $1$1 de cada $4$4 descendentes teria dois genes recessivos (rr) e seria rugosa, correspondendo a $0{,}25$0, comma, 25 ($1/4$1, slash, 4) de probabilidade. Vamos discutir mais sobre como aplicar as regras da probabilidade neste caso.

Em geral, quanto maior for o número de dados usados para calcular uma probabilidade empírica, tais como formas de sementes individuais de ervilha, tanto mais próximo da probabilidade teórica esse número vai chegar.

A regra do produto

Uma regra de probabilidade que é muito útil na genética é a regra do produto, a qual afirma que a probabilidade de dois (ou mais) eventos independentes ocorrerem juntos pode ser calculada multiplicando-se as probabilidades individuais dos eventos. Por exemplo, se você rolar um dado de seis lados de uma vez, você tem uma chance de $1/6$1, slash, 6 de conseguir um seis. Se você rolar dois dados ao mesmo tempo, sua chance de conseguir duas vezes o seis é: (a probabilidade de um seis no dado 1) x (a probabilidade de um seis no dado 2) = $(1/6) \cdot (1/6) = 1/36$left parenthesis, 1, slash, 6, right parenthesis, dot, left parenthesis, 1, slash, 6, right parenthesis, equals, 1, slash, 36.

Em geral, você pode pensar na regra do produto como a regra do "e": se ambos evento X e evento Y devem acontecer para que ocorra um determinado resultado, e se X e Y são independentes um do outro (um não afeta a probabilidade do outro), então você pode usar a regra do produto para calcular a probabilidade do resultado multiplicando as probabilidades de X e Y.

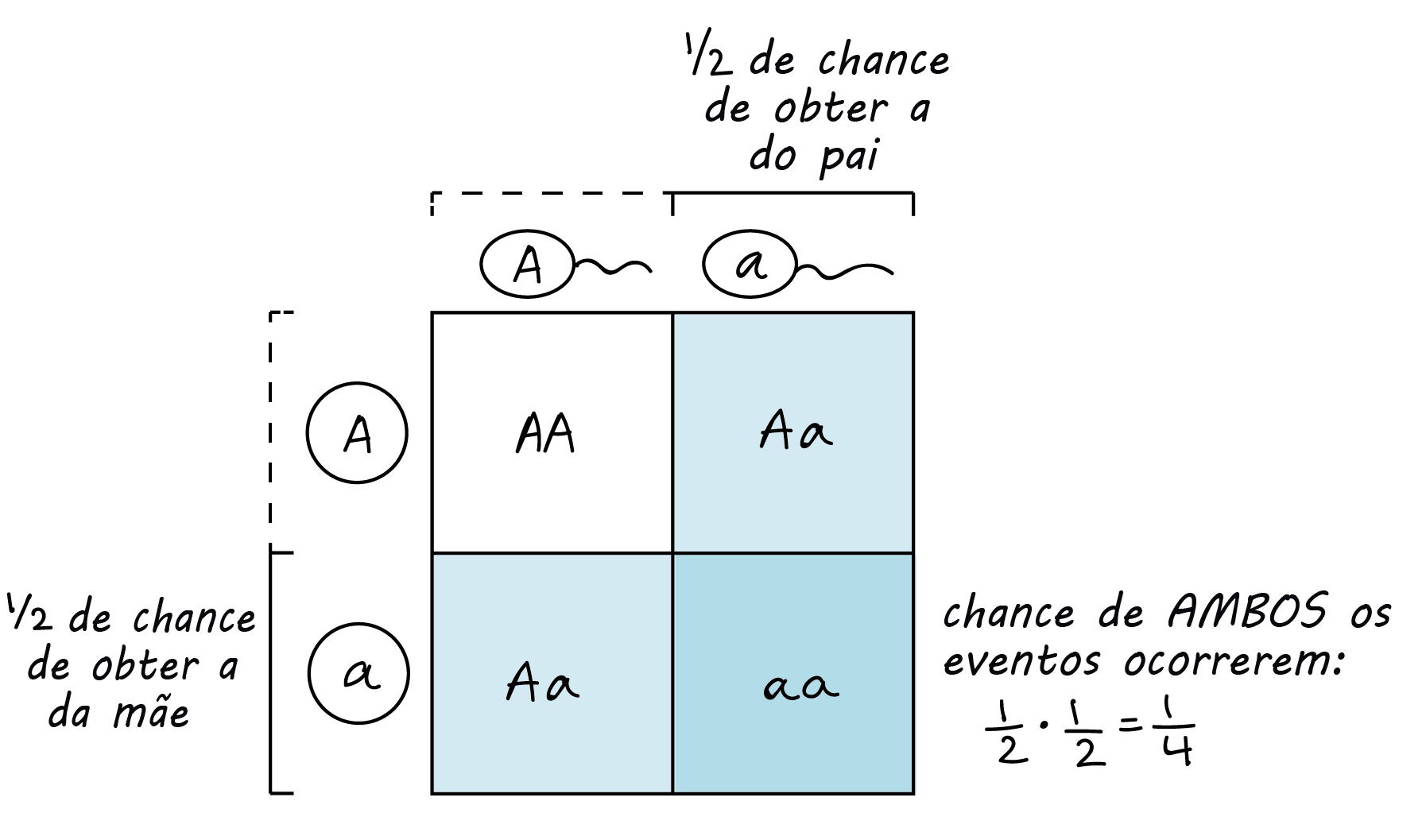
Podemos usar a regra do produto para prever a frequência de eventos de fertilização. Por exemplo, considere o cruzamento entre dois indivíduos heterozigotos (Aa). Quais são as chances de se ter um indivíduo aa na próxima geração? A única forma de se ter um indivíduo aa é se a mãe contribui com um gameta a e o pai contribui com um gameta a. Cada progenitor tem $1/2$1, slash, 2 das chances de fazer um gameta a. Logo, a chance de uma prole aa é: (probabilidade da mãe contribuir a) x (probabilidade do pai contribuir a) = $(1/2) \cdot (1/2) = 1/4$left parenthesis, 1, slash, 2, right parenthesis, dot, left parenthesis, 1, slash, 2, right parenthesis, equals, 1, slash, 4.

Ilustração de como o quadro de Punnett pode representar a regra do produto.

Quadro de Punnett:

		A	a
A		AA	Aa
a		Aa	aa

Há uma 1/2 chance de obtermos um alelo do progenitor masculino, que corresponde à coluna mais à direita do quadro de Punnett. Da mesma forma, há 1/2 chance de obtermos um alelo do progenitor materno, que corresponde à linha inferior do quadro de Punnett. A intersecção desta linha com essa coluna, que corresponde ao quadrado inferior direito da tabela, representa a probabilidade de obtermos o alelo do progenitor materno e do progenitor paterno (1 de 4 quadrados do quadro de Punnett, ou uma chance de 1/4).

Esse é o mesmo resultado que você alcançaria com um quadro de Punnett e, na verdade, utiliza-se o mesmo processo lógico—algo que eu levei anos para perceber. A única diferença é que no quadro de Punnet, faríamos o calculo visualmente: representaríamos a probabilidade $1/2$1, slash, 2 de um gameta a de cada pai como uma de duas colunas (para o pai) e uma de duas linhas (para a mãe). O $1$1-quadrado da intersecção da coluna com a linha (dos $4$4 quadrados totais da tabela) representam a chance de $1/4$1, slash, 4 de se ter um a dos dois progenitores.

A regra da adição de probabilidades

Em alguns problemas genéticos, você pode precisar calcular a probabilidade de que qualquer um de vários eventos ocorra. Nesse caso, você precisará usar outra regra de probabilidade: a regra da soma. Segundo a regra da soma, a probabilidade de que qualquer um de vários eventos mutuamente excludentes ocorra é igual a soma das probabilidades individuais dos eventos.

Por exemplo, se você jogar um dado de seis lados, você terá $1/6$1, slash, 6 de chance de tirar qualquer um dos números, mas você pode tirar apenas um número em cada jogada. Você nunca pode tirar 1 e 6 ao mesmo tempo; os resultados são mutuamente excludentes. Assim, a probabilidade de tirar ou 1 or 6 é: (probabilidade de tirar 1) + (probabilidade de tirar 6) = $(1/6) +(1/6) = 1/3$left parenthesis, 1, slash, 6, right parenthesis, plus, left parenthesis, 1, slash, 6, right parenthesis, equals, 1, slash, 3.

Você pode pensar na regra da soma como a regra do "ou": se um resultado requer que ou o evento X ou o evento Y ocorra, e se X e Y são mutuamente excludentes (se apenas um dos dois eventos podem ocorrem em uma dada situação), então a probabilidade do resultado pode ser calculada somando-se as probabilidades de X e Y.

Como exemplo, vamos usar a regra da soma para prever a fração da prole de um cruzamento Aa x Aa que terá o fenótipo dominante (genótipo AA ou Aa). Nesse cruzamento, há três eventos que podem gerar um fenótipo dominante:

• Dois gametas A se encontram (formando um genótipo AA), ou o gameta
• A da mãe encontra o gameta a do pai (formando um genótipo Aa), ou
• o gameta a da mãe encontra o gameta A do pai (formando um genótipo Aa)

Em cada evento de fertilização, apenas uma dessas três possibilidades pode acontecer (eles são mutuamente excludentes).

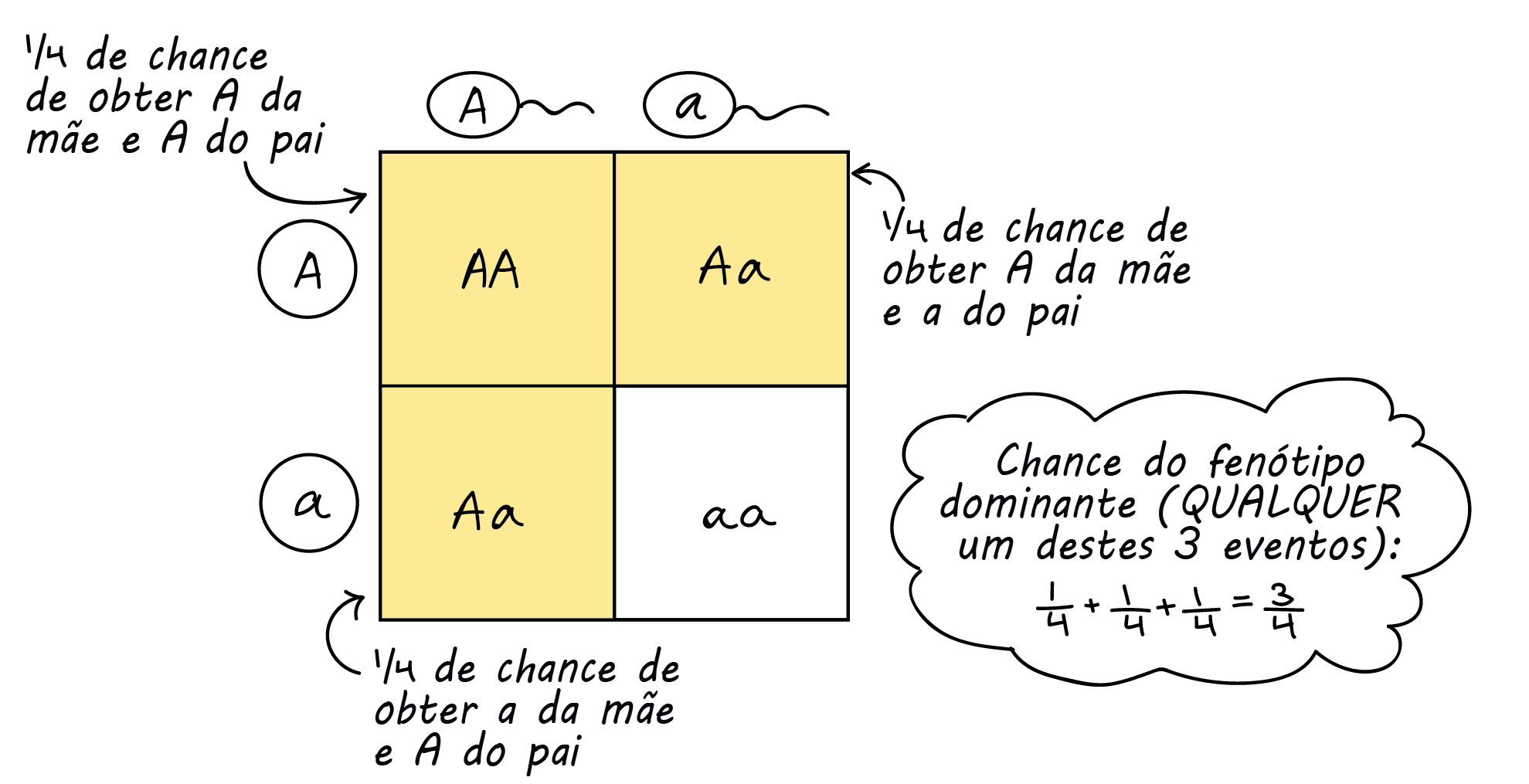
Como essa é uma situação “ou” em que os eventos são mutuamente excludentes, podemos aplicar a regra da soma. Usando a regra do produto, como fizemos acima, podemos determinar que cada evento individual tem a probabilidade de $1/4$1, slash, 4. Então, a probabilidade de uma prole com fenótipo dominante é: (probabilidade de A da Mãe e A do Pai) + (probabilidade de A da Mãe e a do Pai) + (probabilidade de a da Mãe e A do Pai) = $(1/4) + (1/4) + (1/4)= 3/4$left parenthesis, 1, slash, 4, right parenthesis, plus, left parenthesis, 1, slash, 4, right parenthesis, plus, left parenthesis, 1, slash, 4, right parenthesis, equals, 3, slash, 4.

Ilustração de como um quadro de Punnett pode representar a regra da adição.

Quadro de Punnett:

		A	a
A		AA	Aa
a		Aa	aa

Os quadrados em negrito representam eventos cujo resultado é um fenótipo dominante (genótipo AA ou Aa). Em um deles, um espermatozoide A se combina com um óvulo A. No outro, um espermatozoide A se combina com um óvulo a, e no terceiro, um espermatozoide a se combina com um óvulo A. Cada evento tem 1/4 de chance de acontecer (1 de 4 quadrados no quadro de Punnett). A chance de qualquer um desses três eventos ocorrer é de 1/4+1/4+1/4 = 3/4.

Mais uma vez, esse é o mesmo resultado que teríamos com o quado de Punnett. Um dos quatro quadrados do quadro de Punnett possui o homozigoto dominante: AA. Dois quadrados representam heterozigotos, um com o A materno e com o a paterno e outro com a combinação contrária. Cada quadrado é $1$1 de $4$4 quadrados no quadro de Punnett, e como os quadrados não se sobrepõem (eles são mutuamente excludentes), podemos somá-los ($1/4 + 1/4 + 1/4 = 3/4$1, slash, 4, plus, 1, slash, 4, plus, 1, slash, 4, equals, 3, slash, 4) para ter a probabilidade de proles com o fenótipo dominante.

A regra do produto e a regra da adição

Regra do produto	Regra da soma
Para eventos independentes X e Y, a probabilidade ($P$P) de ambos ocorrerem (X e Y) é $P(X) \cdot P(Y)$P, left parenthesis, X, right parenthesis, dot, P, left parenthesis, Y, right parenthesis.	Para eventos mutuamente excludentes X e Y, a probabilidade ($P$P) de um ocorrer (X ou Y) é $P(X) + P(Y)$P, left parenthesis, X, right parenthesis, plus, P, left parenthesis, Y, right parenthesis.

Aplicação das regras da probabilidade a cruzamentos diíbridos

O cálculo direto de probabilidade não tem grandes vantagens em relação ao quadro de Punnett para cenários de herança de um único gene. (De fato, se você prefere aprender visualmente, você pode considerar o cálculo direto mais complicado). Contudo, as probabilidades brilham quando analisamos o comportamento de dois ou mais genes.

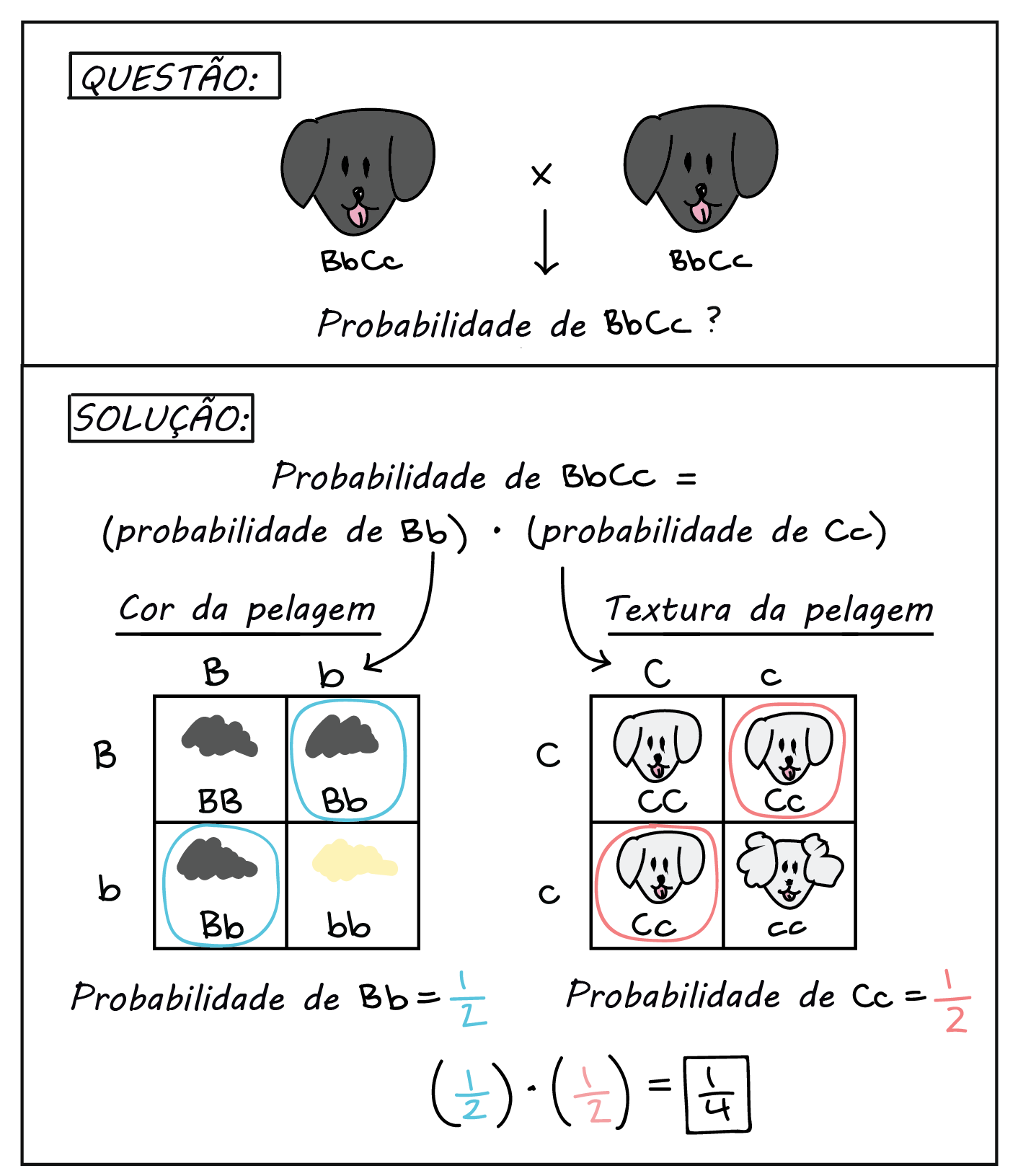
Por exemplo, vamos imaginar que cruzamos dois cachorros com o genótipo BbCc, em que o alelo dominante B especifica pelos de cor preta (contra b, que especifica pelos amarelos) e o alelo dominante C especifica pelo liso (contra c, pelo encaracolado). Supondo que os dois genes combinam-se de maneira independente e não estão ligados ao sexo, como podemos prever o número de filhotes BbCc nessa prole?

Uma abordagem é desenhar $16$16-quadrados no quadro de Punnett. Para um cruzamento envolvendo dois genes, o quadro de Punnett ainda é uma boa estratégia. Alternativamente, podemos usar um atalho com quatro quadrados do quadro de Punnett e a aplicação da regra do produto. Com essa técnica, nós dividimos a pergunta em duas questões menores, cada uma relacionada com um evento genético:

1. Qual a probabilidade de se obter o genótipo Bb?
2. Qual a probabilidade de se obter o genótipo Cc?

Para que um filhote tenha o genótipo BbCc, devem ocorrer dois eventos: o filhote deve receber os alelos Bb, e os alelos Cc. Os dois eventos são independentes porque os genes se combinam independentemente (um não afeta a herança do outro). Assim, uma vez que calculamos a probabilidade de cada evento genético, podemos multiplicar essas probabilidades usando a regra do produto para obter a probabilidade do genótipo de interesse (BbCc).

Diagrama ilustrando como podemos usar os quadros de Punnett de 2X2, juntamente com a regra do produto para determinar a probabilidade de um genótipo específico em um cruzamento diíbrido.

Painel superior:

Pergunta: quando dois cachorros BbCc cruzam, qual é a probabilidade de se ter um descendente BbCc?

Painel inferior:

Resposta: probabilidade de BbCc = (probabilidade de Bb) x (probabilidade de Cc)

Quadro de Punnett para cor do pelo:

		B	b
B		BB	Bb
b		Bb	bb

Probabilidade do genótipo Bb: 1/2

Quadro de Punnett para textura do pelo:

		C	c
C		CC	Cc
c		Cc	cc

Probabilidade do genótipo Cc: 1/2

Probabilidade de BbCc = (probabilidade de Bb) x (probabilidade de Cc) Probabilidade de BbCc = (1/2) x (1/2) = 1/4

Para calcular a probabilidade de se obter o genótipo Bb, podemos desenhar $4$4-quadrados no quadro de Punnett, usando apenas os alelos dos pais para a cor de pelo, como visto acima. Através do quadro de Punnett, vemos que a probabilidade do genótipo Bb é $1/2$1, slash, 2 (outra alternativa seria calcular a probabilidade de Bb usando a regra do produto para as contribuições dos gametas dos dois progenitores e a regra da soma para a combinação dos dois gametas que geram Bb). Usando um quadro de Punnett similar para os alelos de textura de pelo dos pais, a probabilidade de se ter o genótipo Cc também é $1/2$1, slash, 2. Para se chegar à probabilidade total do genótipo BbCc, podemos simplesmente multiplicar as duas probabilidades, obtendo a probabilidade total de $1/4$1, slash, 4.